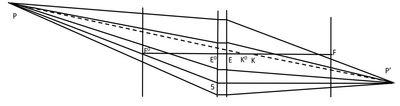
Nodal Points and cardinal points

The work on "far peripheral vision" led to finding that the nodal point of the eye can be used to scale the retina to very large angles, even though it is only defined for very small angles and flat surfaces. This seemed to be widely known, or assumed, but with no published explanation. 

Papers have now been published that explore this topic, and these show that the corneal curvature and the retinal curvature are factors that make this possible. The cornea curves around toward incoming light, input angles are rescaled by a fairly constant factor of about 0.8 at the exit pupil, and then the retina curves around to meet the image. When the image is viewed from the nodal point, which is approximately at the posterior surface of a crystalline lens, the angle to the nodal point is approximately the same as the input angle. 

The work on nodal points led to finding a lack of clarity about how the term efl is defined.  For a lens in air, there is really just a "focal length", yet it has become common to use the term "effective focal length" for efl, and it is not clear how this came about.

The issue that is probably being addressed is that when the image is in fluid, the overall optical effect is described using the focal length divided by the refractive index. This is important for lenses in the eye, but it is not the situation for the majority of lenses. However, for a lens in air the index would be 1, so the same term could be used for all lenses. It seems likely that the use of efl became common when computers began to be widely used for optical design. 

Looking at historical references, the word "equivalent" has been more commonly used, with "equivalent focal length" being a definition for efl. This probably originally described the focal length for a thin "equivalent" lens that had a similar optical effect to a thick lens or a compound lens in air (though the extra word was not necessary). The optical effect of a lens that normally forms an image in fluid, when the object is in air, can be described by an equivalent lens in air using the efl, where:

  focal length is the distance from the principal plane to the image, and

  efl = (focal length)/index. 

Even this does not seem to be a universal definition though, which is unfortunate for something as fundamental to lenses as the term "focal length".

The rationale for using the word "effective" rather than "equivalent" for efl is unclear, but it was included in Warren Smith's Modern Optical Engineering in 1966, along with comments that "focal length" = "effective focal length" = efl. It seems likely that only lenses in air were being considered for this, and that efl was preferred over f or fl because early raytrace computer software was already using 3-letter terms. If there is a clear historical reference for either of these things it would be good to find them (why efl rather than f; why effective rather than equivalent).